DFS & BFS
- 경로 찾기 문제의 상황에 따라 DFS와 BFS를 그래프 알고리즘으로 사용할 수 있습니다.
- 그래프는 꼭짓점을 연결하는 노드와 가장자리로 구성된 데이터 구조이며 그래프를 순회한다는 것은 꼭짓점에서 시작하여 모든 꼭짓점을 순서대로 한 번 방문하는 것을 의미합니다.
- 그래프 순회를 위한 두 알고리즘 방문한 노드검사를 받아야 합니다. (활성화하지 않으면 무한 루프의 위험)
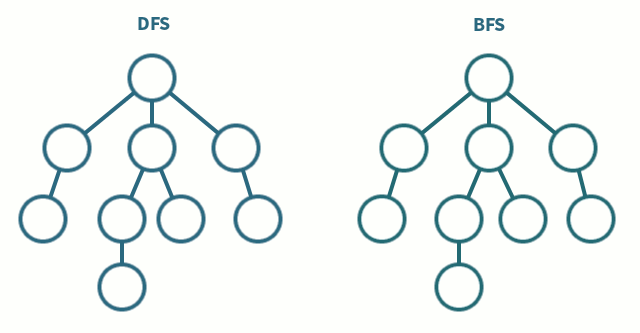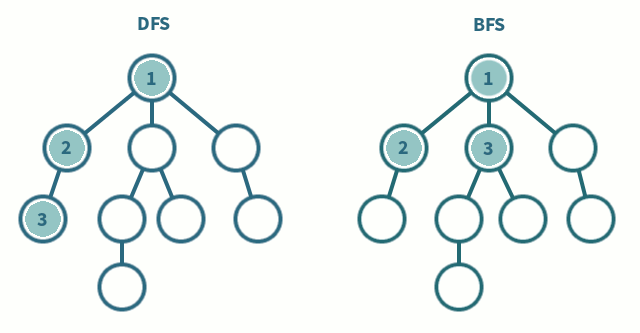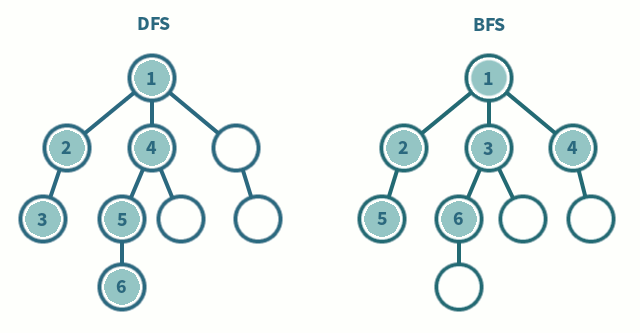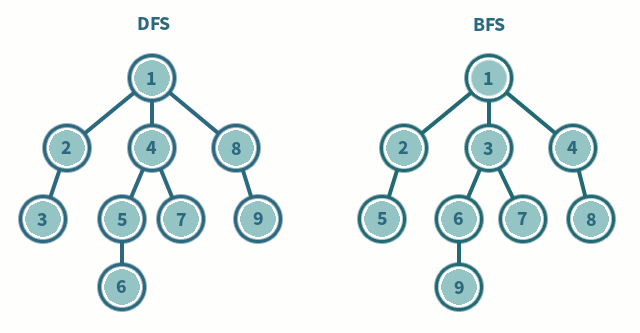
깊이 우선 탐색(DFS)
- 루트 노드(또는 임의의 노드)에서 시작하여 다음 분기로 이동하기 전에 모든 분기를 통과(미로와 유사)
- 스택 또는 재귀 함수(재귀 알고리즘의 형태로)로 구현
- 모든 경로를 방문해야 하는 경우적합
- 시간 복잡도(V는 정점, E는 에지)
- 인접 행렬: O(V^2)
- 이웃 목록: O(V+E)
너비 우선 탐색(BFS)
- 따라서 먼저 루트 노드(또는 임의의 노드)에서 이웃 노드로 검색합니다.
- 예어(노드 주변에서 검색해야 하기 때문에) → 선입선출(FIFO) 원칙에 따라 검색으로 구현
- 최소 비용우선권이 주어질 때 적합
- 주로 두 노드 사이의 최단 경로필요한 것을 찾기 위해
- 재귀적으로 작업
- 시간적 복잡성
- 인접 행렬: O(V^2)
- 이웃 목록: O(V+E)
그리디 알고리즘
- 그리디 알고리즘
- 문제 해결 과정에서 우리는 언제라도 답에 도달하는 것이 최적인 방식으로 진행합니다.
- 문제의 본질이 동일하고 동일한 전략을 반복적으로 사용할 수 있는 경우 적용
- 이전 결정이 후속 결정에 영향을 미치지 않는 경우
- 최종 솔루션이 하위 문제에 대한 솔루션과 동일한 조건인 경우
- 장점: 다른 최적 솔루션 계산 알고리즘에 비해 저렴한 비용(빠름)
- 단점: 최적의 가치를 찾는 순간이기 때문에 항상 최적의 솔루션을 찾는 것은 불가능합니다.